不要理睬在路边和你搭话的人。 如果已经理睬了,不要相信他说的自己的动人故事。 如果相信了他说的动人故事,也不要拿他给你的东西,不然一会儿你还不回去。 如果拿了他给你的东西,也不要买他的东西,尽量尽快脱身。 如果实在傻而想买他的东西,...
在你的Arch Linux笔记本上畅快使用NVIDIA显卡,包括Vulkan
上回(《在你的 Arch Linux 笔记本上畅快使用 NVIDIA 显卡》)说到如何在Arch Linux上配置NVIDIA和Intel双显卡,但还留有一个问题未解决,就是Vulkan应用会唤醒独显,导致启动和退出一些应用时因需要唤...
分析一种利用腾讯文档传播的新型诈骗
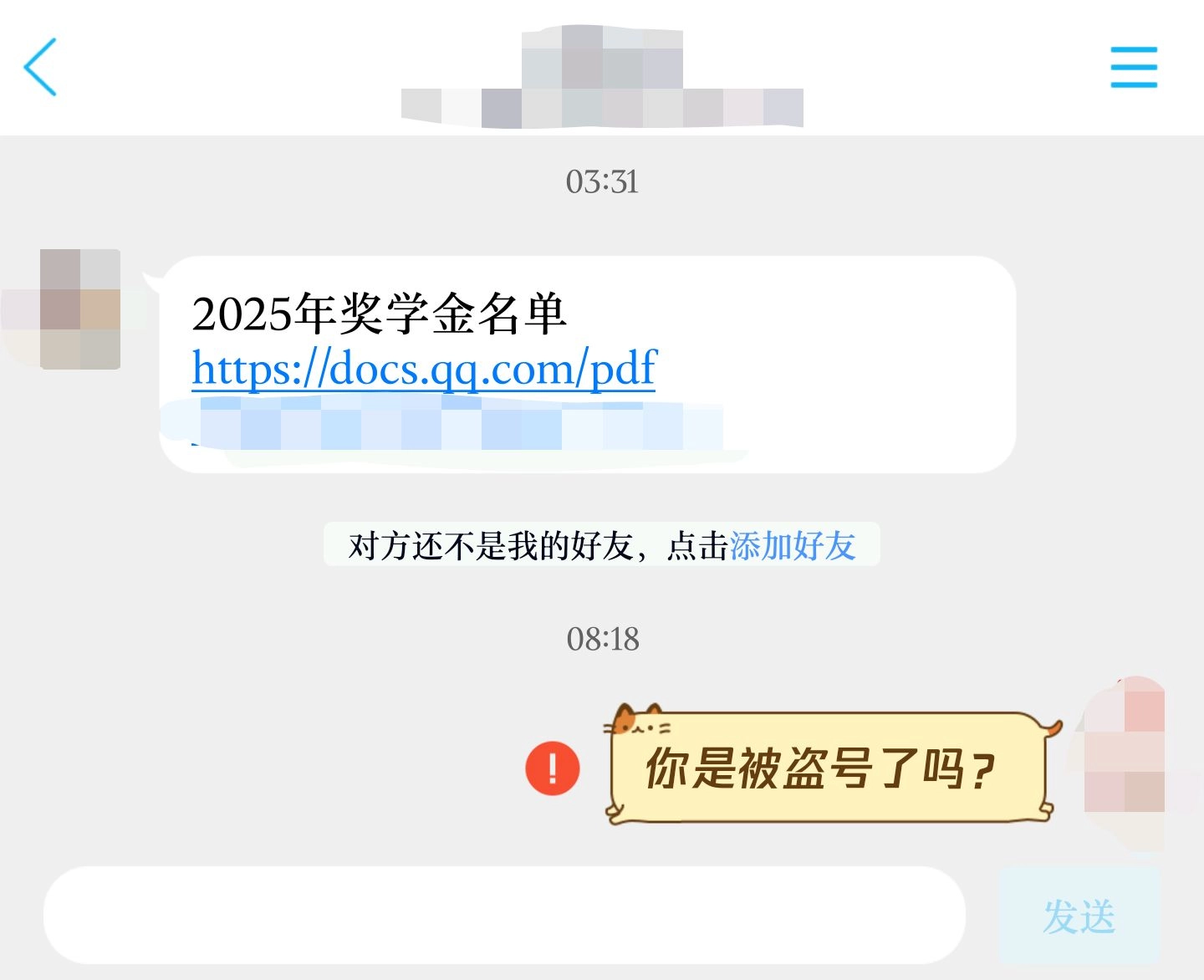
近日我频繁收到通过QQ私信分享的腾讯文档链接,不法分子利用马化腾的妈和腾讯的客服的存在状态必定相同的特点,以腾讯文档为跳板进行钓鱼。遇到这种情况时,大家务必提高警惕。本文将粗浅地分析一下这种诈骗的技术手段。 快速跳转到防范建议 诈骗文...
为什么 Unicode 有「私用区字符不会在无此字体其他电脑上显示」的规定?
题目描述: 也就是说,例如私用区的生造汉字、符号等,仅自己电脑能显示,其他电脑如果不装载此私用区就无法显示,是技术不足,还是另有隐情? 原文链接:https://www.zhihu.com/question/12008172105...
在华为手表上听音乐吧——FLAC 到 MP3 带标签转换教程
华为手表支持通过手机同步音乐文件进行离线播放,而且支持 FLAC 格式。但是,你真的想在手表那么小的存储空间里放大量的 FLAC 文件吗……本文将教你如何将 FLAC 文件转换为 MP3,并保留原有的标签信息供「华为运动健康」App ...
在你的 Arch Linux 笔记本上畅快使用 NVIDIA 显卡
新购机械革命旷世 X Pro 游戏笔记本电脑一台,搭载 NVIDIA GeForce RTX 5070 Ti Laptop 显卡,到手后便安装了 Arch Linux。此乃我初次安装 Arch Linux,亦是初次使用带有独立显卡的电...
纸飞机在雨中飞——对 Telegram 的一些思考
以下内容整理自我在网上聊天室中的发言。 距离 Telegram CEO Pavel Du Rove 最初被法国政府提出指控已有数周。有文章因 Telegram 不默认启用端到端加密而对其隐私性提出质疑。以下是我的观点。 Teleg...
震惊!早起不叠被子有这么多好处!
你还在每天早上费劲地叠被子吗?快停下!现在,一项震惊世人的研究表明,早起不叠被子竟然有许多意想不到的好处! 1. 告别尘螨,呼吸更自由! 我们都知道,被子是尘螨的乐园。而每天叠被子,就如同将它们关在一个温暖潮湿的密闭空间里,让它们...
“反转”不是进步,真相需要维护
本文是考场作文,得分 50 分。我自以为颇有意义,现将原文如实呈现,整理如下,供大家参考阅读,望不吝赐教。 阅读下面材料,根据要求写作。(60 分) 近些年在互联网传播场域中,“反转”式新闻连番上演。在这个时代,对同一事件的报道常常...
记一次有惊无险的 Linux 下根分区大小调整经历
你将在本文中读到以下内容:使用 fdisk 工具恢复分区顺序、删除交换分区后需要的修复工作 如果你只是想了解如何扩容磁盘,请看文章最后的结论部分。 请注意,请不要效仿本文中的错误操作。只有你遇到了相似的问题,才可以运用文章中的补救措施...